Lidé jsou totiž často uchváceni tím, jaké detaily lze dalekohledem na Měsíci vidět. Skutečnost je ovšem taková, že i ten teoreticky nejmenší rozlišitelný objekt na Měsíci má při pozorování běžným amatérským dalekohledem o průměru 150 mm rozměr necelé 2 kilometry. Přitom americká vlajka na Měsíci je jen malý obdélník o stranách 0,91 a 1,52 metru. Na to tedy běžný dalekohled ani zdaleka nestačí. Ve skutečnosti bychom potřebovali dalekohled s průměrem téměř 200 metrů, zatímco největší dalekohled na světě má průměr „pouze“ 10,4 metru! Čili spatření americké vlajky na Měsíci dalekohledem je zcela nemožné.

Zdroj: NASA
Zkusme se ale podívat na jiné, větší objekty, které Američané na Měsíci zanechali. Například na lunární vozítko, které má na délku 3,1 metru. I na něj bychom však potřebovali dalekohled s průměrem 85 metrů. Největším objektem, který se dostal na povrch, byl samotný lunární modul, jehož spodní základna na Měsíci zůstala, neboť sloužila jako startovací rampa pro horní oddělitelnou část. Ta měla napříč kolem 9,5 metru, avšak i tato hodnota by vyžadovala dalekohled o průměru asi 30 metrů. Ze Země zkrátka nelze pozorovat žádné pozůstatky po přistání na Měsíci.
Zároveň dodejme, že jsme uvažovali nejmenší možné rozměry dokonale vyrobených dalekohledů, kdy by byl daný objekt sotva rozlišitelný jako pouhý bod. Pro identifikaci objektu bychom ale zřejmě potřebovali ještě citelně jemnější rozlišení, tedy ještě mnohem větší dalekohledy. Kromě toho tyto výpočty nezahrnují vliv atmosféry, čili je lze vztáhnout jedině na dalekohledy na oběžné dráze, jako je známý Hubbleův teleskop, případně na dalekohledy s adaptivní optikou, které umí vliv atmosféry eliminovat. Bavíme se ovšem o optickém limitu, který je daný povahou světla a tím že podléhá ohybu, kdy se samotný kruhový otvor chová jako štěrbina o konečném rozměru; rozlišení na fotografii v pixelech se totiž dále odvíjí i od ohniskové vzdálenosti a použitého snímače.
Nemusíte však zoufat, že by se žádným způsobem nešlo podívat na pozůstatky po přistání. Sice to není možné dalekohledem ze Země, ale umí to automatické sondy na oběžné dráze kolem Měsíce, a nejlépe to zatím dokázala sonda Lunar Reconnaissance Orbiter (LRO). Té se v roce 2009 podařilo nasnímat místa přistání s rozlišením až půl metru na pixel. Sonda sice nedisponuje žádným velkým dalekohledem, průměr je pouze 195 mm, ale fotila z výšky jen několika desítek kilometrů nad povrchem. Výsledné fotografie si lze prohlédnout na stránkách NASA.
Zajímá vás, jak se dospěje k uvedeným hodnotám v článku? Čtěte dále a seznámíte se s postupem výpočtu.
Prvně je potřeba uvést vztah pro výpočet úhlového rozlišení dalekohledu α. To se spočítá jako
[pmath]alpha=1.22*lambda/D[/pmath]
kde λ je vlnová délka světla a D je průměr dalekohledu. Pokud obě hodnoty dosadíme v metrech, vyjde úhlové rozlišení dalekohledu v radiánech. Vlnovou délku jsme ve výpočtech uvažovali přibližně uprostřed spektra viditelného světla, a sice 550 nanometrů. Pro úplnost dodejme, že tento úhel odpovídá úhlové vzdálenosti například dvou hvězd, které bychom byli schopni poměrně jednoznačně rozlišit jako dva světelné zdroje. Pro menší vzdálenosti by se hvězdy začaly výrazněji slévat do sebe a od určití chvíle bychom už vůbec nebyli schopni říct, že se jedná o dvě hvězdy.
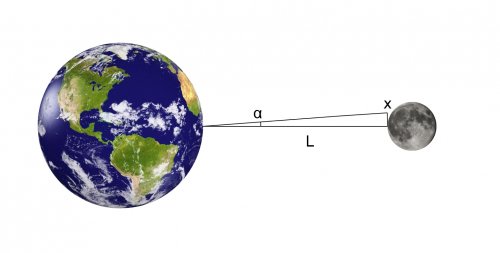
Další pokračování už je snadná trigonometrická úloha s pravoúhlým trojúhelníkem, kde známe úhel z rozlišení dalekohledu a vzdálenost od pozorovaného objektu, což je v našem případně vzdálenost Země-Měsíc, jejíž střední hodnota činí 384 400 km.
Dospějeme tedy ke vztahu
[pmath]tan alpha=x/L[/pmath]
kde x je velikost pozorovaného objektu a L vzdálenost objektu. Ale s ohledem na to, že pro takto malé úhly se tangens úhlu přibližná rovná přímo hodnotě úhlu, můžeme jednoduše psát jen
[pmath]alpha=x/L[/pmath]
Pokud takto α dosadíme do prvního vzorce pro rozlišení dalekohledu, získáme konečný vztah
[pmath]1.22*lambda/D=x/L[/pmath]
z něhož lze již snadno vyjádřit x, pokud známe průměr dalekohledu a zajímá nás, jak velký objekt uvidíme. Nebo naopak můžeme vyjádřit D, pokud známe velikost objektu a zajímá nás, jak velký dalekohled pro jeho spatření potřebujeme.